Estimated reading time: 2 minutes
This post is the third in a series of posts about machine learning and showcasing the benefits ArangoML adds to your machine learning pipelines. In this post we:
- Introduce bootstrapping and bias-variance concepts
- Estimate and analyze the variance of the model from part 2
- Capture the metadata for this activity with arangopipe
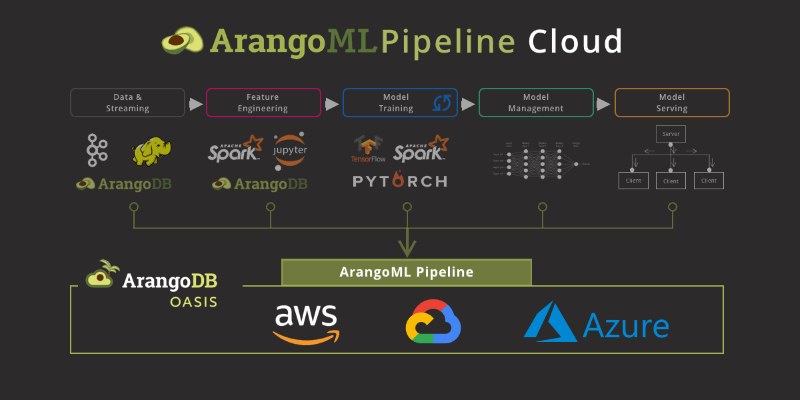
Posts in this series:
ArangoML Part 1: Where Graphs and Machine Learning Meet
ArangoML Part 2: Basic Arangopipe Workflow
ArangoML Part 3: Bootstrapping and Bias Variance
ArangoML Part 4: Detecting Covariate Shift in Datasets
ArangoML Series: Intro to NetworkX Adapter
ArangoML Series: Multi-Model Collaboration
These posts will hopefully appeal to two audiences:
- The first half of each post is for beginners in machine learning
- The second half for those already using machine learning
We decided to do it this way to provide a jumping-off point for those interested in machine learning while still showing useful examples for those who already have a machine learning pipeline.
Hear More from the Author
ArangoDB Graph Database Syntax Part 1 – Traversal
Continue Reading
Neo4j Fabric: Scaling out is not only distributing data
ArangoML Pipeline Cloud – Managed Machine Learning Metadata Service
